Question

In right △ABC with right angle B, m∠A=(3x−8)° and m∠C=(x−2)°.

What is m∠A?

Question Options:


47°


67°


25°


92

Answer 1

Add both and set it equal to 90

Answer 2

Option 2nd is correct

67°

Explanation:

Given that:

In right △ABC with right angle B.

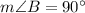`m \angle B = 90^(\circ)`, m∠A=(3x−8)° and m∠C=(x−2)°.

We know that the sum of all the measures of a triangle is 180 degree

In triangle ABC

⇒
`m\angle A+ m\angle B+ m\angle C = 180^(\circ)`

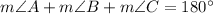
Substitute the values we have;

`3x-8+90^(\circ)+x-2 = 180^(\circ)`

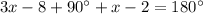
Subtract 90 degree from both sides we have;

`3x-8+x-2 = 90^(\circ)`

Combine like terms;

`4x-10= 90^(\circ)`

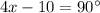
Add 10 to both sides we have;

`4x=100^(\circ)`

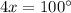
Divide both sides by 4 we have;

`x=25^(\circ)`

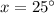
then;

m∠A=(3(25)−8)° = (75-8)° = 67°

Therefore, the measure of angle A is, 67°