Question

The collision between two gas molecules with different masses results in the velocity of the first molecule decreasing by 1/4. If the collision is elastic, which of the following statements is true?

A. The velocity of the second molecule will increase by a factor of 4.
B. The velocity of the second molecule will increase by a factor of 16.
C. The velocity of the second molecule will decrease by a factor of 16.
D. The velocity change of the second molecule depends on both the mass and the velocity of the first molecule.
Please explain why it is the right answer too

Answer 1

Answer: The correct option is D.

Step-by-step explanation: We are given two gas molecules with different masses. The collision between them is elastic, hence the Total Kinetic energy of the system is conserved.

Initial Kinetic Energy:

`K.E_i=(1)/(2)m_1u_1^2+(1)/(2)m_2u_2^2`

Final Kinetic Energy:

`K.E_f=(1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2`

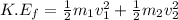
where,

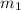`m_1` = mass of first molecule

`m_2` = mass of second molecule

`u_1` = initial velocity of first molecule

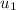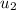`u_2` = initial velocity of second molecule

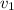`v_1` = final velocity of first molecule

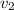`v_2` = final velocity of second molecule

Elastic Collision:

`K.E_i=K.E_f`

That is,

`(1)/(2)m_1u_1^2+(1)/(2)m_2u_2^2=(1)/(2)m_1v_1^2+(1)/(2)m_2v_2^2`

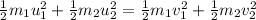
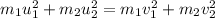`m_1u_1^2+m_2u_2^2=m_1v_1^2+m_2v_2^2` .....(1)

We are given in the question that the final velocity of first molecule is decreased by 1/4, which means:

`v_1=(u_1)/(4)`

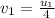
Putting this value in equation 1 , we get

`m_1u_1^2+m_2u_2^2=(m_1u_1^2)/(16)+m_2v_2^2`

`m_1u_1^2-(m_1u_1^2)/(16)+m_2u_2^2=m_2v_2^2`

`m_1((15u_1^2)/(16))+m_2u_2^2=m_2v_2^2`

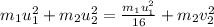
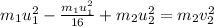
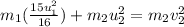
taking
`m_2` on other side, we get

`(m_1)/(m_2)((15u_1^2)/(16))+u_2^2=v_2^2`

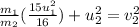
From the above relation, it is visible that the velocity change of the second molecule depends on both mass and velocity of the first molecule.