Answer:
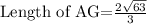
Explanation:
Please follow the diagram in attachment.
As we know median from vertex C to hypotenuse is CM
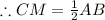
We are given length of CG=4
Median divide by centroid 2:1
CG:GM=2:1
Where, CG=4
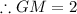 ft
ft
Length of CM=4+2= 6 ft
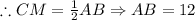
In
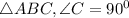
Using trigonometry ratio identities
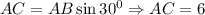 ft
ft
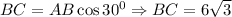 ft
ft
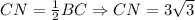 ft
ft
In
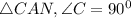
Using pythagoreous theorem

Length of AG=2/3 AN
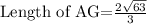 ft
ft