To find the ratio of the areas, we are obviously going to first need to find the areas of the inner and outer squares. The outer square has a side length of
 because we are
because we are
 units away from 0 on the x-axis. Thus, the area of the outer square is
units away from 0 on the x-axis. Thus, the area of the outer square is
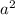 .
.
We can see that a right triangle is formed by part of the x-axis, part of the y-axis, and the side of the inner square. Thus, we can find the length of the inner square through the Pythagorean Theorem, which is
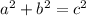 , where
, where
 and
and
 are the legs of the right triangle and
are the legs of the right triangle and
 is the hypotenuse. The lengths of the legs of the right triangle in the picture are
is the hypotenuse. The lengths of the legs of the right triangle in the picture are
 and
and
 . We can use the Pythagorean Theorem to find the other side length.
. We can use the Pythagorean Theorem to find the other side length.


We have now found that the side length of the inner square is
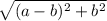 . Thus, the area of the inner square is
. Thus, the area of the inner square is
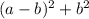 .
.
Using the two areas we just found, we can say that the ratio of the area of the inner square to the area of the outer square is
 , or choice A.
, or choice A.