The distributive property says that the following is true:

In our problem, we will consider the term outside (or
 in the first equation) to be
in the first equation) to be
 and we will consider the expression inside the parentheses to be
and we will consider the expression inside the parentheses to be
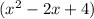 . To use the distributive property, we are going to apply the outside term to all terms within the second expression. This is represented as:
. To use the distributive property, we are going to apply the outside term to all terms within the second expression. This is represented as:
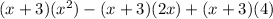
We can now use the distributive property again to simplify the new expression:

The answer is x³ + x² - 2x + 12.