Answer: The opposite sides of quadrilateral WXYZ are not parallel.
Step-by-step explanation:
It is given that WXYZ is quadriatral with vertices W(-1,-1) X(-3,-1) Y(-2,4) Z(2,3).
Since WXYZ is a quadrilateral, therefore WX and YZ are opposite sides. Similarly XY and WZ are opposite sides.
We know that the slope of parallel lines are equal.
The slope of line passing through the point
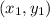 and
and
 is calculated as,
is calculated as,

Find the slope of WX and YZ.
The two vertex W(-1,-1) and X(-3,-1).
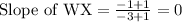
The two vertex Y(-2,4) and Z(2,3).
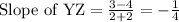
Since slope of WX and YZ is not equal, therefore WX and YZ are not parallel.
Find the slope of WZ and XY.
The two vertex W(-1,-1) and Z(2,3).
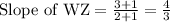
The two vertex X(-3,-1) and Y(-2,4).
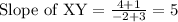
Since slope of WZ and XY is not equal, therefore WZ and XY are not parallel.