Question

How many whole numbers are there, whose squares and cubes have the same number of digits?

Answer 1

there are only 4 whole numbers whose squares and cubes have the same number of digits.

Explanations:

let 0, 1, 2 and 4∈W (where W is a whole number), then

`0^2=0`,
`0^3=0`,

`1^2=1`,
`1^3=1`,

`2^2=4`,
`2^3=8`,

`4^2=16`,
`4^3=64`.

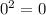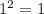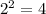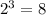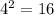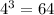You can see from the above that only four whole numbers are there whose squares and cubes have the same number of digits