Question

A sample of an unknown compound contains 82.63% C, and 17.37% H. Determine the empirical formula.

Answer 1

The actual amount of substance doesn’t matter for this problem, so assume an easy mass of compound using the percentages: 82.63 g C and 17.37 g H. There is also no need to worry about significant figures in an empirical formula problem.

Find the number of moles of each element:

`(82.63 \text{ g C})(\frac{1 \text{ mol C}}{12.011 \text{ g C}} )=6.88 \text{ mol C}\\(17.37 \text{ g H})(\frac{1 \text{ mol H}}{1.0078 \text{ g H}} )=17.2 \text{ mol H}`

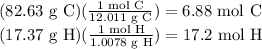
Find the ratio of the elements, and simplify until there are whole numbers that you can put into the empirical formula.

`\frac{17.2 \text{ mol H}}{6.88 \text{ mol C}} =\frac{2.5 \text{ mol H}}{1 \text{ mol C}}=\frac{5 \text{ mol H}}{2 \text{ mol C}}`

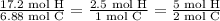
There are 5 mol H for every 2 mol C, so the empirical formula should be
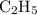`{\text{C}}_2{\text{H}}_5`.