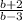Answer:
Simplify the expression:
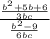
The top expression given in the above fraction is Numerator and the bottom expression is called Denominator.
Now, multiply the numerator and denominator by
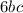 ;
;
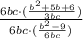
Simplify:
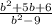
Now, Factor the numerator
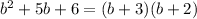 and denominator
and denominator
 ;
;
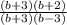
Now, cancel the common factor (b+3) we get;
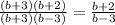
Therefore, the simplify expression of
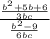 is,
is,