Question

The former Sears Tower in Chicago is 443m tall. Suppose a book is dropped from the top of the building. What would be the book's velocity a point 221m above the ground?

Answer 1

here we can use energy conservation

like initial kinetic + potential energy is always conserved and it will be same at all points

so we can say

`KE_i + PE_i = KE_f + PE_f`

`(1)/(2)mv_i^2 + mgh_1 = (1)/(2)mv_f^2 + mgh_2`

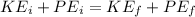
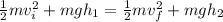
now we can plug in all the given values in it

`v_i = 0`

`h_1 = 443 m`

`h_2 = 221 m`

`(1)/(2)m*0 + m*9.8*443 = (1)/(2) m*v_f^2 + m*9.8*221`

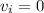
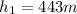
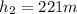
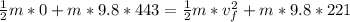
now divide whole equation by mass "m"

`9.8*443 = (1)/(2) v_f^2 + 9.8*221`

`2175.6 = (1)/(2)v_f^2`

`v_f = 65.96 m/s`

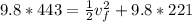
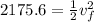
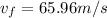
so final speed will be 65.96 m/s