Question

A bus driver follows a morning route and an afternoon route each day. Because there are more cities on the morning route, the average speed is 12 miles per hour less than the afternoon route. The driver covers 70 miles on the morning route in the same amount of time as she covers 100 miles on the afternoon route. Find her average speed on the afternoon route.

A. 28 miles per hour
B. 40 miles per hour
C. 36 miles per hour
D. 51 miles per hour

Answer 1

Answer: The correct option is B, i.e., 40 miles per hour.

Step-by-step explanation:

Let the speed of bus in the afternoon route be x.

From the given information the average speed is 12 miles per hour less than the afternoon route. So, the speed of bus in the morning route is x-12.

`\text{Average Speed}=\frac{\text{Total Distance}}{\text{Total Time}}`

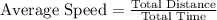
So,

`\text{Total Time}=\frac{\text{Total Distance}}{\text{Average Speed}}`

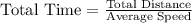
Time taken by bus in morning route is,

`\text{Total Time}=(70)/(x-12)`

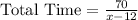
Time taken by bus in afternoon route is,

`\text{Total Time}=(100)/(x)`

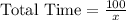
Since it is given that the time is same, so

`(70)/(x-12)=(100)/(x)`

`70x=100(x-12)`

`70x=100x-1200`

`30x=1200`

`x=40`

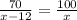
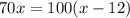
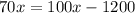
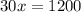
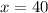
Since x represents the speed of bus in afternoon route, therefore the correct option is B, i.e., 40 miles per hour.