Question

Find the exponential regression equation that best fits the data (10,4), (12,20), (12,35), and (16,300)

A. y=0.003(2.04)^x

B. y=2.04(0.003)^x

C. y=11.27(1.00)^x

D. y=1.00(11.27)^x

Answer 1

We are exponential equation in form
`y=AB^x`.

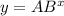We need to find the values of A and B.

We are given points (10,4), (12,20), (12,35), and (16,300).

Let us check equation in option y=0.003(2.04)^x by plugging those given points in that equation.

Plugging x=10

y=0.003(2.04)^10 = 3.74475.

Plugging x= 12.

y=0.003(2.04)^12 = 15.58416

Plugging x=16.

y= 0.003(2.04)^16 = 269.9.

Now, if we check option B y=2.04(0.003)^x, we have decay factor there 0.003.

So, it would be a decay function.

If we check y=11.27(1.00)^x we have 1.00 so it's not growing exponentially.

And 1.00(11.27)^x is growing at extremely high rate.

Therefore, correct option would be A. y=0.003(2.04)^x.