Question

Find the area of a plane figure bounded by lines

1.y=x^2+2x+4, y=x+6
2.y=x^2+6x+5, y= - x^2-6x-11

Answer 1

Answer: 4.5

Explanation:

First, find the points of intersection by solving the system.

y = x² + 2x + 4

y = x + 6

Solve by substitution:

x² + 2x + 4 = x + 6 ⇒ x² + x - 2 = 0 ⇒ (x + 2)(x - 1) = 0 ⇒ x = -2, x = 1

Now, integrate from x = -2 to x = 1

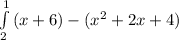`\int\limits^1_2 {(x+6)-(x^(2)+2x+4) } \,` the bottom of the integral is -2

=
`\int\limits^1_2 {x+6-x^(2)-2x-4 } \,`

=
`\int\limits^1_2 {-x^(2)-x+2 } \,`

=
`(-x^(3))/(3) - (x^(2))/(2)+2x\int\limits^1_2 {} \,`

=
`((-1^(3))/(3) - (1^(2))/(2)+2(1)) - ((-(-2)^(3))/(3) - ((-2)^(2))/(2)+2(-2))`

=
`((-1)/(3) - (1)/(2) +2) - ((8)/(3) -(4)/(2) -4)`

=
`(-9)/(3) + (3)/(2) +6`

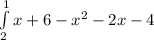
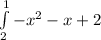
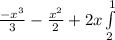
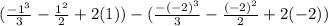
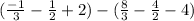
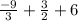
= -3 + 1.5 + 6

= 4.5