Answer:

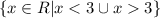

Explanation:
To find the domain of a rational expression like
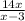 you need to find out where the denominator is 0 because you cannot divide by 0
you need to find out where the denominator is 0 because you cannot divide by 0
So, take the denominator x - 3 and set it to zero and solve for x
x - 3 = 0
x = 3
So the domain is all real numbers but where x = 3. You can write this in a few different ways in set notation.
---------------------------------------
NOTE
R = real numbers
 = element of
= element of
| = such that
---------------------------------------

Or you could write it this way
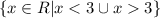
Or you could write it this way
