Question

A species of beetles grows 32% every year. Suppose 100 beetles are released into a field. How many beetles will there be in 10 years?

A species of beetles grows 32% every year. Suppose 100 beetles are released into a field.
How many beetles will there be in 20 years? A species of beetles grows 32% every year. Suppose 100 beetles are released into a field.
About when will there be 100,000 beetles?

Answer 1

Javier must carefully record and describe all of the characteristics of his beetle.

Explanation:

Javier might have found a new species of beetle. But he will only be able to figure this out if he has carefully recorded all of the details of the beetle. So Javier must closely observe it, and take careful notes. After he has done this, he can compare his description to that of known species.

Answer 2

Given that a species of beetles grows 32% every year.

So growth rate is given by

r=32%= 0.32

Given that 100 beetles are released into a field.

So that means initial number of beetles P=100

Now we have to find about how many beetles will there be in 10 years.

To find that we need to setup growth formula which is given by

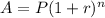`A=P(1+r)^n` where A is number of beetles at any year n.

Plug the given values into above formula we get:

`A=100(1+0.32)^n`

`A=100(1.32)^n`

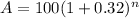
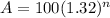
now plug n=10 years

`A=100(1.32)^(10)=100(16.0597696605)=1605.97696605`

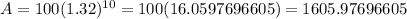
Hence answer is approx 1606 beetles will be there after 20 years.

Now we have to find about how many beetles will there be in 20 years.

To find that we plug n=20 years

`A=100(1.32)^(20)=100(257.916201549)=25791.6201549`

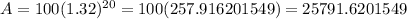
Hence answer is approx 25791 beetles will be there after 20 years.

Now we have to find time for 100000 beetles so plug A=100000

`A=100(1.32)^n`

`100000=100(1.32)^n`

`1000=(1.32)^n`

`log(1000)=n*log(1.32)`

`(\log\left(10000\right))/(\log\left(1.32\right))=n`

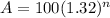
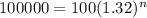
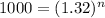
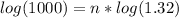
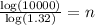
33.174666862=n

Hence answer is approx 33 years.