Question

Triangle ABC has vertices at A(−1 , 2), B(4, 2), and C(3, −1). Classify the triangle according to the side lengths.

A) equilateral
B) isosceles
C) right
D) scalene

Answer 1

B) isosceles

Explanation:

Answer 2

B) Isosceles

Explanation:

The given triangle has vertices at A(-1,2), B(4,2) and C(3,-1).

We must first determine the length of the sides of the triangle, before we can classify it.

We apply the distance formula to find length of the sides.

`|AB|=√((4--1)^2+(2-2)^2)`

`\Rightarrow |AB|=√((4+1)^2+(2-2)^2)`

`\Rightarrow |AB|=√(5^2+(0)^2)`

`\Rightarrow |AB|=√(25)`

`\Rightarrow |AB|=5 units`.

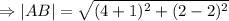
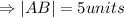The length of side BC

`|BC|=√((3-4)^2+(-1-2)^2)`

`\Rightarrow |BC|=√((-1)^2+(-3)^2)`

`\Rightarrow |BC|=√(1+9)`

`\Rightarrow |BC|=√(10)`

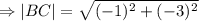
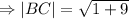
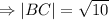
The length of side AC

`|AC|=√((3--1)^2+(-1-2)^2)`

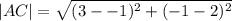
We simplify to obtain;

`|AC|=√((3+1)^2+(-3)^2)`

`\Rightarrow |AC|=√((4)^2+(-3)^2)`

`|AC|=√(16+9)`

`|AC|=√(25)`

`|AC|=5\:units`

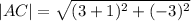
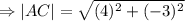
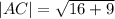
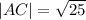
Since
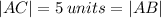`|AC|=5\:units=|AB|`, the given triangle is an isosceles triangle.

The correct answer is