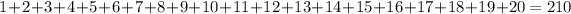Question

For the Rule of 78, for a 12-month period, the last term in the sequence is 12 and the series sums to 78.

For an 14 month period, the last term is and the series sum is .

For a 16 month period, the last term is and the series sum is .

For a 20 month period, the last term is and the series sum is.

Answer 1

We can solve this question using the formula below-

The formula for sum of n terms is,

`S_n=(n)/(2) [2a+(n-1)d]`

For 14 months the last term is 14 and its sum is,

Here a = 1 and d = 1

`S_(14)=(14)/(2) [2(1)+(14-1)(1)]`

`S_(14)=7(15)=105`

For 16 months the last term is 16 and its sum is,

Here a = 1 and d = 1

`S_(16)=(16)/(2) [2(1)+(16-1)(1)]`

`S_(16)=8(17)=136`

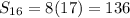
OR

We can also solve this using simple addition like-

1. For a 14 month period the last term in the sequence is 14 and the series sum is;

`1+2+3+4+5+6+7+8+9+10+11+12+13+14= 105`

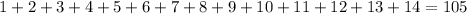
2. For a 16 month period, the last term is 16 and the series sum is;

`1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16= 136`

3. For a 16 month period, the last term is 20 and the series sum is;

`1+2+3+4+5+6+7+8+9+10+11+12+13+14+15+16+17+18+19+20=210`