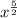The expression is:
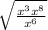
We will use following steps to simplify it:
Step 1:
Use product property of exponents:
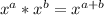
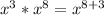
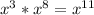
That gives us the expression:
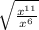
Step 2:
Use division property of exponents:

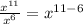
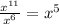
This simplifies the expression:

Step 3:
Writing the square root as power 1/2:
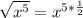
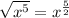
Answer:
The final simplified form in x^n form is :