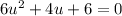We are given the equation:
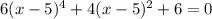 ..........(1)
..........(1)
Now we have to write it in quadratic form using substitution.
The general form of quadratic equation is given by:

So let us say
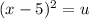 .......(2)
.......(2)
Plugging the value of (x-5)² from equation (2) in (1),
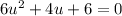
Answer : Option B.