Tony and Mike, factored the trinomial
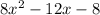
Tony factored it as 4(x - 2)(2x + 1) and
Mike factored it as (x - 2)(8x + 4)
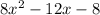
GCF is 4. We factor out 4
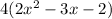
2*-2=-4. We find out two factors whose product is -4 and sum is -3
two factors are -4 and 1. Split middle term -3x using two factors
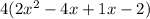
Group first two terms and last two terms
![4[(2x^2 - 4x) + (1x - 2)]](https://img.qammunity.org/2019/formulas/mathematics/high-school/qfap0cdpxhndb3vu1qrcu4gqgl5i5l21vb.png)
Factor out GCF from each group
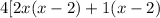
4(2x+1)(x-2)
Tony factored it correctly
Mike factored it as (x − 2)(8x + 4)
Mike factor 8x+4 further. GCF of 8 and 4 is 4
So it becomes 4(2x+1)
Mike not factored it completely