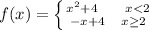2 Answers

Alexandrecosta · Answer 1 · 2019-09-28T21:05:27+0000

Answer:

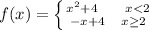
$f(x)=\left \{ {{x^2+4}\ \ \ \ \ x<2 \atop {-x+4}\ \ \ x\geq 2}\right$

C is correct

Explanation:

In the given graph function break at point x=2.

Left side about point x=2 is parabolic and right side straight line.

So, it would be piece wise function.

For parabola:

vertex: (0,4) and passing point (2,8)

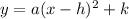
y=a(x-h)^2+k

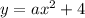
y=ax^2+4

a=1

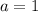
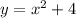y=x^2+4 For x<2

For straight line:

Twp points (4,0) and (2,2)

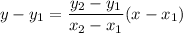
y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)

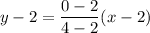
y-2=(0-2)/(4-2)(x-2)

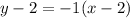
y-2=-1(x-2)

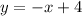y=-x+4 For x≥2

Hence, The piece wise function will be

$f(x)=\left \{ {{x^2+4}\ \ \ \ \ x<2 \atop {-x+4}\ \ \ x\geq 2}\right$

Please log in or register to add a comment.