Question

The ratio of the prices of Emma's phone to Sophie's phone is 7:8. If Sophie's phone costs $640, how much should the prices of their phones decrease in order to have a ratio of 9:11 ?

Answer 1

For the ratio between the price of the phones to be 9:11, the price of Emma's phone must decrease from $ 560 to $ 523.66. That is, the price of Emma's phone should decrease $ 36,364

Explanation:

To answer this question, call x on Emma's phone and z on Sophie's phone.

We know that the price relationship between x and z is 7: 8

This means that:

`(7)/(8) =(x)/(z)`

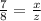
We know that the price of Sophie's phone is $ 640

Entoces z = 640

Now we clear x

`(7)/(8) =(x)/(640)\\ x =640}(7)/(8)=560\\ x = 560`

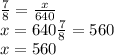
Then, if the new relationship is 9:11 then:

`(9)/(11) =(x)/(640)`

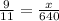
x = $523,636

For the ratio between the price of the phones to be 9:11, the price of Emma's phone must decrease from $ 560 to $ 523.66. That is, the price of Emma's phone should decrease $ 36,364

Answer 2

Let cost of Emma's phone = x

Given that cost of Sophie's phone = 640

Then ratio of their phones cost will be x:640 or x/640

Given that ratio of their phones cost is 7:8 or 7/8

So both ratios will be equal.

`(x)/(640)=(7)/(8)`

`x=(7)/(8)*640`

x=560

So the new ratio of the cost of their phones will be 560:640

Now we have to find about how much should the prices of their phones decrease in order to have a ratio of 9:11.

So let that decreased amount is k then we will get equation :

`(560-k)/(640-k)=(9)/(11)`

11(560-k)=9(640-k)

6160-11k=5760-9k

6160-5760=11k-9k

400=2k

200=k

Hence final answer is prices of their phones should decrease by 200 in order to have a ratio of 9:11.