Answer:
12.68%
Explanation:
To calculate effective annual interest rate we need to use the following formula:
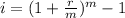
Where, 'i' is the effective annual interest rate
'r' is the annual rate of interest
'm' is the frequency of compounding.
When there is continuous compounding the effective annual rate uses the following formula:
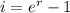
In our case we would are assume that there is continuous compounding since no information regarding the frequency of compounding is given:
Plugging r=12%=0.12, we get:
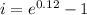
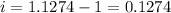
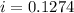
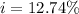
Therefore, the effective annual interest rate is 12.74%.