Answer:
x = -7 and x = 4
Explanation:
Note, I am taking the polynomial equation as
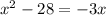
Otherwise it does not become a polynomial of one variable and cannot be solved
Zeros of a polynomial are the values of x where the polynomial value itself is 0
Standard equation for a polynomial of degree 2 is ax² + bx + c = 0 where a, b and c are constants
Degree is the highest exponent. Here the highest exponent is 2 so the polynomial has degree 2. Such a polynomial is called a quadratic polynomial
So we first have to convert
x² - 28 = - 3x into this form ax² + bx + c
1. Add 3x to both sides
x² - 28 + 3x = -3x + 3x =0
==> x² + 3x - 28 = 0
With a = 1, b = 3 and c = -28
2. Factor x² + 3x - 28 = 0
Here a = 1, b = 3 and c = -28
Factoring means find two expressions x+a and x +b such that (x + a) (x + b) = x² + 3x - 28 = 0
Then we can state that
x + a = 0 ==> x = -a as one solution
x + b = 0 ==> x = -b as the other solution
To factor, find two numbers m and n(could be negative) such that mn = c and m + n = b
28 has factors 7 and 4 so that is a good start
-28 = -7 x 4 or could also be 7 x -4
How do we choose?
Add both and see what gives you +3
-7 + 4 = -3 Nope
7 + -4 = 7-4 = 3 YES
So the factors are 7 and -4
(x + m) = (x + 7)
(x + n) = (x -4)
So the original quadratic polynomial becomes
(x + 7)(x -4) =
This means
x + 7 = 0 ==> x = -7
x - 4 = 0 ==> x = 4
So the solutions(also called roots) of x² + 3x - 28 = 0 are:
x = -7 and x = 4
Both the above values satisfy the quadratic equation