The slopes of the lines passing through the given points are: 1.
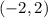 and
and
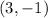 :
:
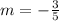 . 2.
. 2.
 and
and
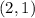 :
:
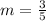 . 3.
. 3.
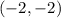 and
and
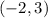 : The slope is undefined (vertical line).
: The slope is undefined (vertical line).
To calculate the slope m of a line given two points
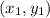 and
and
 , you can use the formula:
, you can use the formula:
![\[m = (y_2 - y_1)/(x_2 - x_1)\]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/a9sq6l7oc01b5vm998ph2npbm0phmpyx83.png)
Let's apply this formula to the given points:
1. For points (-2,2) and (3,-1):
![\[m = (-1 - 2)/(3 - (-2)) = (-3)/(5)\]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/jcni7azzkxtk9aplrqxrc42n1ly5wg6751.png)
2. For points (-3,-2) and (2,1):
![\[m = (1 - (-2))/(2 - (-3)) = (3)/(5)\]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/dxxm423ib8yiin9m20s946tu7sepft2ae0.png)
3. For points (-2,-2) and (-2,3):
![\[m = (3 - (-2))/((-2) - (-2)) = (5)/(0)\]](https://img.qammunity.org/2019/formulas/mathematics/middle-school/o1kts8sgqj2020fjiykjgq89b221zfdfp7.png)
The slope for the third set of points is undefined because the denominator becomes zero, indicating a vertical line. The first two sets of points have slopes of
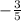 and
and
 respectively.
respectively.