Question

How do you determine the solution of a systems of linear equations from a graph?

Question 2 options:

A.The solution is the x-intercept


B.The solution is the y-intercept


C.The solution is the intersection of both lines


D.The solution cannot be determined from a graph

Answer 1

Suppose you have two lines, and consider the system of their equations:

`\begin{cases} y = mx+q\\y=m'x+q'\end{cases}`

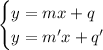
Suppose that a certain point
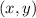`(x,y)` belongs to the first line. This means that his x and y coordinates follow the rule
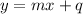`y=mx+q`. Similarly, if another point
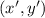`(x',y')` belongs to the second line, his x and y coordinates follow the rule
`y'=m'x'+q'`.

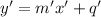A system is solved by the points that satisfy both equations simultaneously. But satisfying an equation means to belong to the graph that the equation represents.

So, the solution to the system is the point that belongs to both lines, i.e. that satisfies both equations.