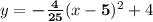Question

NO LINKS!

The WBHS golf team was out hitting some golf balls on the weekend. Matt hit the ball off the ground and followed it a parabolic path reached a height of 4 feet. If ball hit the ground in 10 seconds, write the equation that would model the situation

h(t)=___(x - __)^2 + ___​

Answer 1

Answer:
`y = \boldsymbol{-(4)/(25)}(x - \boldsymbol{5})^2 + 4`

========================================================

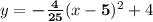
Step-by-step explanation:

The instructions don't mention it, but I'm assuming that the height of 4 feet is the max height the of the ball.

If so, then this is the vertex of the parabola.

The ball is on the ground when x = 0 and x = 10. The x coordinate of the vertex is the midpoint of those two roots. So it's at x = 5.

Overall, the vertex is (h,k) = (5,4)

The equation

y = a(x-h)^2 + k

becomes

y = a(x-5)^2 + 4

Next, we plug in the root (x,y) = (10,0) since the ball hits the ground when x = 10. Let's solve for 'a'

y = a(x-5)^2 + 4

0 = a(10-5)^2 + 4

0 = 25a + 4

25a = -4

a = -4/25

We could have used (x,y) = (0,0) and we'd end up with the same 'a' value.

Therefore, the height function is

`y = \boldsymbol{-(4)/(25)}(x - \boldsymbol{5})^2 + 4`