Answer:
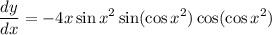
General Formulas and Concepts:
Calculus
Differentiation
- Derivatives
- Derivative Notation
Basic Power Rule:
- f(x) = cxⁿ
- f’(x) = c·nxⁿ⁻¹
Derivative Rule [Chain Rule]:
![\displaystyle (d)/(dx)[f(g(x))] =f'(g(x)) \cdot g'(x)](https://img.qammunity.org/2019/formulas/mathematics/high-school/ijuuby0owovgvvmkyt63pxr8cpkn8j9mgp.png)
Explanation:
Step 1: Define
Identify
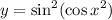
Step 2: Differentiate
- Basic Power Rule [Derivative Rule - Chain Rule]:
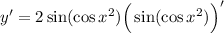
- Trigonometric Differentiation [Derivative Rule - Chain Rule]:
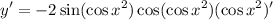
- Trigonometric Differentiation [Derivative Rule - Chain Rule]:
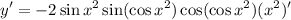
- Basic Power Rule:
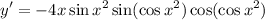
Topic: AP Calculus AB/BC (Calculus I/I + II)
Unit: Differentiation