Question

Two airplanes leave an airport at the same time.The velocity of the first airplane is 700 m/h at a heading of 31.3 the velocity of the second is 570 m/h at the heading of 134° how far apart are they after three hours?

Answer 1

Planes are 2985.48 miles far after 3 hours.

Step-by-step explanation:

Let right represents positive x- axis and up represent positive y - axis. Horizontal component is i and vertical component is j.

We have velocity of the first airplane is 700 m/h at an angle 31.3° to the horizontal.

So Velocity of first plane = 700 cos 31.3 i + 700 sin 31.3 j

= (598.12 i + 363.66 j) m/h

We also have velocity of the second airplane is 570 m/h at an angle 134° to the horizontal.

Velocity of second plane = 570 cos 134 i + 570 sin 134 j

= (-395.96 i + 410.02 j) m/h

Displacement of first plane after 3 hours = Velocity * Time

= (598.12 i + 363.66 j) *3

= (1794.36 i + 1090.98 j) mi

Displacement of second plane after 3 hours = (-395.96 i + 410.02 j)*3

= (-1187.88 i + 1230.06 j) mi

Displacement vector between two planes = (1794.36 i + 1090.98 j) - (-1187.88 i + 1230.06 j)

= (2982.24 i - 139.08 j) mi

Magnitude of displacement =
`√(2982.24^2+(- 139.08)^2) =2985.48 mi`

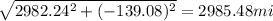
So planes are 2985.48 miles far after 3 hours.

Answer 2

Here in order to find out the distance between two planes after 3 hours can be calculated by the concept of relative velocity

`v_(12) = v_1 - v_2`

here

speed of first plane is 700 mi/h at 31.3 degree

`v_1 = 700 cos31.3\hat i + 700 sin31.3\hat j`

`v_1 = 598.12\hat i + 363.7\hat j`

speed of second plane is 570 mi/h at 134 degree

`v_2 = 570 cos134 \hat i + 570 sin134 \hat j`

`v_2 = -396\hat i + 410\hat j`

now the relative velocity is given as

`v_(12) = (598.12 + 396)\hat i + (363.7 - 410)\hat j`

`v_(12) =994.12\hat i -46.3 \hat j`

now the distance between them is given as

`d = v* t`

`d = (994.12 \hat i - 46.3 \hat j)* 3`

`d = 2982.36\hat i - 138.9\hat j`

so the magnitude of the distance is given as

`d = √(2982.36^2 + 138.9^2)`

`d = 2985.6` miles

so the distance between them is 2985.6 miles