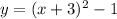2 Answers

Ospahiu · Answer 1 · 2019-04-25T13:13:43+0000

For this case we have:

The equation in vertex form of the parabola is given by:

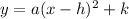
$y = a (x-h) ^ 2 + k\\$

The vertex is (h, k) and is given by the highest or lowest point of the parabola, in this case it is observed that it is
$(h, k) = (- 3, -1)\\$

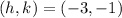
Thus, the equation is given by:

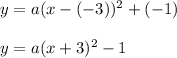
$y = a (x - (- 3)) ^ 2 + (- 1)\\\\y = a (x + 3) ^ 2-1\\$

We look for the value of a, substituting a point of the parabola in the equation in the form of vertex, we will take the point
$(x, y) = (0,8)\\$

Substituting we have:

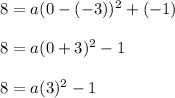
$8 = a (0 - (- 3)) ^ 2 + (- 1)\\\\8 = a (0 + 3) ^ 2-1\\\\8 = a (3) ^ 2-1\\$

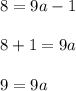
$8 = 9a-1\\\\8 + 1 = 9a\\\\9 = 9a\\$

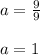
$a = (9)/(9)\\\\a = 1\\$

Thus, the equation of the parabola is given by:

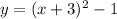
$y = (x + 3) ^ 2-1\\$

Answer:

Please log in or register to add a comment.