Question

List all subsets of the following set [1]?

Answer 1

{ } and {1}

Explanation:

Let as consider the given set

`S=\{1\}`

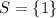
We need to find tall subsets of the given set.

Number of subsets of a set =
`2^n`

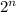
where, n is the number of elements in that set.

In the given set the number of elements = 1.

Number of subsets of given set =
`2^1=2`

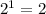
So, the number of subsets of given set is 2.

If all elements of set A are included in set B, then A is subset of set B.

`A\subseteq B`

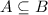
Empty set or ∅ is the subset of all sets and each set is the subset of itself. It means

`\{ \}\subseteq \{1\}`

`\{ 1\}\subseteq \{1\}`

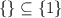
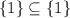
Therefore, subsets of given set are { } and {1}.

Answer 2

ANSWER

{},{1}

EXPLANATION

The given set has one element. So it has
`2^1=2` subsets.

These are,

{} and {1}.

That is, the null set and the set itself.

Remember that, the null set is a subset of every set and every set is a subset of itself.