Answer:
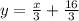
Explanation:
Hello, I think I can help you with this
Step 1
let line 1
y=-3x+5
this equation is in the form y= mx+b, where m is the slope,Hence
-3x=mx
-3=m
m(1)=-3
Step 2
two lines are perpendicular if the product of their slopes is equal to -1
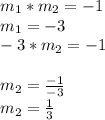
Step 3
find the equation of the line
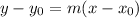
Let
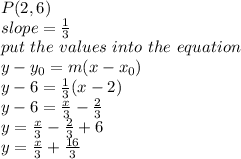
Have a nice day.