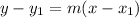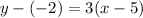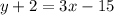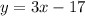Answer:
y = 3x - 17
Explanation:
Here is the point-slope form of the equation of a line.
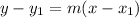
If you are given a slope, m, and a point on the line, (x1, y1), you just plug in the values into the equation above, and you get the equation of the line.
In your problem, you are given a point on the line, (5, -2). Now you need the slope of the line. Your line is perpendicular to the given line. The slopes of perpendicular lines are negative reciprocals. If you know the slope of a line, the slope of its perpendicular is found by flipping the fraction and changing the sign.
The given line has slope -1/3.
Flip -1/3 to get -3.
Now change the sign to get 3.
The slope of the line you need is 3. The line passes through point (5, -2).
Now we use the point-slope equation and we plug in the values we have.