Question

A coffee merchants want to make 6 pounds of a blend of coffee costing five dollars per pound. The blend is made using a six dollar per pound grade coffee and a three dollar per pound grade of coffee. How many pounds of each of these grades should be used?

Answer 1

We should use 4 pounds of $6 coffee and 2 pounds of $3 coffee for the blend.

Explanation:

The blend should,

Cost = $5

Weigh = 6 pounds.

Lets take the weight of $6 coffee as
`x` pounds

And lets take the weight of $3 coffee as
`y` pounds.

Lets write an equation for the weight of the blend,

`x+y=6` <---------- 1st equation.

`(6x+3y)/(x+y) =5`

=
`6x+3y=5x+5y`

=
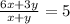
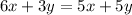
`x=2y` <---------- 2nd equation

We can substitute to x in 1st equation from 2nd equation,

⇒
`2y+y=6`

=
`2y+y=6`

=
`3y=6`

=
`y=2`

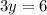
We can substitute y value to 2nd equation to find x,

⇒
`x=2y`

=
`x=2*2`=
`x=4`

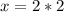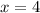
Therefore, we should use 4 pounds of $6 coffee and 2 pounds of $3 coffee for the blend.