Question

How do you solve this problem?

Answer 1

The particle has acceleration vector

`\vec a=\left(-2.0\,(\mathrm m)/(\mathrm s^2)\right)\,\vec\imath+\left(4.0\,(\mathrm m)/(\mathrm s^2)\right)\,\vec\jmath`

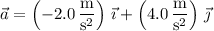
We're told that it starts off at the origin, so that its position vector at
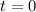`t=0` is

`\vec r_0=\vec0`

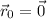
and that it has an initial velocity of 12 m/s in the positive
`x` direction, or equivalently its initial velocity vector is

`\vec v_0=\left(12\,(\mathrm m)/(\mathrm s)\right)\,\vec\imath`

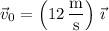
To find the velocity vector for the particle at time
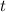`t`, we integrate the acceleration vector:

`\vec v=\vec v_0+\displaystyle\int_0^t\vec a\,\mathrm d\tau`

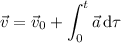
`\vec v=\left[12\,(\mathrm m)/(\mathrm s)+\displaystyle\int_0^t\left(-2.0\,(\mathrm m)/(\mathrm s^2)\right)\,\mathrm d\tau\right]\,\vec\imath+\left[\displaystyle\int_0^t\left(4.0\,(\mathrm m)/(\mathrm s^2)\right)\,\mathrm d\tau\right]\,\vec\jmath`

`\vec v=\left[12\,(\mathrm m)/(\mathrm s)+\left(-2.0\,(\mathrm m)/(\mathrm s^2)\right)t\right]\,\vec\imath+\left(4.0\,(\mathrm m)/(\mathrm s^2)\right)t\,\vec\jmath`

Then we integrate this to find the position vector at time
`t`:

`\vec r=\vec r_0+\displaystyle\int_0^t\vec v\,\mathrm d\tau`

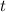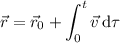
`\vec r=\left[\displaystyle\int_0^t\left(12\,(\mathrm m)/(\mathrm s)+\left(-2.0\,(\mathrm m)/(\mathrm s^2)\right)t\right)\,\mathrm d\tau\right]\,\vec\imath+\left[\displaystyle\int_0^t\left(4.0\,(\mathrm m)/(\mathrm s^2)\right)t\,\mathrm d\tau\right]\,\vec\jmath`

`\vec r=\left[\left(12\,(\mathrm m)/(\mathrm s)\right)t+\left(-1.0\,(\mathrm m)/(\mathrm s^2)\right)t^2\right]\,\vec\imath+\left(2.0\,(\mathrm m)/(\mathrm s^2)\right)t^2\,\vec\jmath`

Solve for the time when the
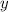`y` coordinate is 18 m:

`18\,\mathrm m=\left(2.0\,(\mathrm m)/(\mathrm s^2)\right)t^2\implies t=3.0\,\mathrm s`

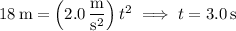
At this point, the
`x` coordinate is

`\left(12\,(\mathrm m)/(\mathrm s)\right)(3.0\,\mathrm s)+\left(-1.0\,(\mathrm m)/(\mathrm s^2)\right)(3.0\,\mathrm s)^2=27\,\mathrm m`

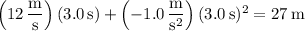
so the answer is C.