Question

Describe the end behavior of the following function:

Answer 1

The correct answer is that the function starts high and ends low.

Explanation:

First we need to check for the highest power in a term. Since it is 5, which is an odd number, we know that they start and end in different places.

Next, we determine where it finishes based on the coefficient of that term, which is -1. Since it is negative, we know it finishes down. Since they are different, this means it starts up

Answer 2

A ) The graph of the function start high and ends low .

Explanation:

Given : f(x) =
`-x^(5) +x^(2) -x`.

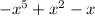To find : Describe the end behavior of the following function.

Solution : We have given function

f(x) =
`-x^(5) +x^(2) -x`.

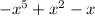We can see the Degree = 5 ( Odd) , Leading coefficient = negative .

By the End Behavior Rule : If the degree odd and leading coefficient is negative then the left side of graph would be up and right would be down.

Therefore, A ) The graph of the function start high and ends low .