Question

Quadrilateral RSTU has vertices R(1,3), S(4,1), T(1,-3) and U(-2,-1). Is it true or false that this is a rectangle because the diagonals are congruent and the sides RS and ST are perpendicular?

Answer 1

Given vertices ofQuadrilateral RSTU as R(1,3), S(4,1), T(1,-3) and U(-2,-1).

We need to check if diagonals are congruent.

The coordinates of verticales diagonal RT are R(1,3) and T(1,-3).

The coordinates of verticales diagonal SU are S(4,1), and U(-2,-1),

By applying distance formula:

`\mathrm{Compute\:the\:distance\:between\:}\left(x_1,\:y_1\right),\:\left(x_2,\:y_2\right):\quad √(\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2)`

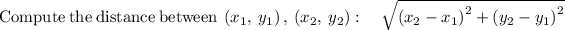
RT =
`=√(\left(1-1\right)^2+\left(-3-3\right)^2)`=
`√(36)`

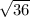
RT = 6

SU
`=√(\left(-2-4\right)^2+\left(-1-1\right)^2)`.

`=2√(10)`.

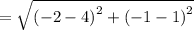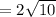Diagonal RT is not congruent to Diagonal SU.

Therefore, Quadrilateral RSTU is not a rectangle because the diagonals are not congruent.

So, it is False.