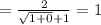Question

Calculate the limit values:

a) lim
   x → ∞ ln (x ^ 2 + 2) / x

  b) lim
      x → 0 tan x / x

c) lim
    x → 0 e 2x - 1 - 2x / x 2 2

d) lim
     x → ∞? (√x ^ 2 + 2x - x)

Answer 1

a) This particular limit is of the indeterminate form,

`( \infty )/( \infty )`
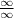
if we plug in infinity directly, though it is not a number just to check.

If a limit is in this form, we apply L'Hopital's Rule.

's

`Lim_(x \rightarrow \infty ) ( ln(x ^(2) + 1 ) )/(x) = Lim_ {x \rightarrow \infty } (( ln(x ^(2) + 1 ) ) ')/(x ' )`
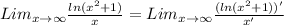
So we take the derivatives and obtain,


`Lim_ {x \rightarrow \infty } ( ln(x ^(2) + 1 ) )/(x) = Lim_(x \rightarrow \infty ) ( (2x)/(x^(2) + 1) )/(1)`

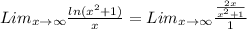
Still it is of the same indeterminate form, so we apply the rule again,


`Lim_(x \rightarrow \infty ) ( ln(x ^(2) + 1 ) )/(x) = Lim_(x \rightarrow \infty ) ( 2 )/(2x)`

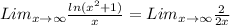
This simplifies to,


`Lim_(x \rightarrow \infty ) ( ln(x ^(2) + 1 ) )/(x) = Lim_(x \rightarrow \infty ) ( 1 )/(x) = 0`

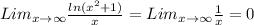
b) This limit is also of the indeterminate form,


`(0)/(0)`
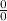
we still apply the L'Hopital's Rule,


`Lim_ {x \rightarrow0 }( tanx)/(x) = Lim_ {x \rightarrow0 } ( (tanx)')/(x ' )`


`Lim_ {x \rightarrow0 }( tanx)/(x) = Lim_ {x \rightarrow0 } ( \sec ^(2) (x) )/(1 )`

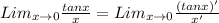
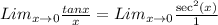
When we plug in zero now we obtain,


`Lim_ {x \rightarrow0 }( tanx)/(x) = Lim_ {x \rightarrow0 } ( \sec ^(2) (0) )/(1 ) = (1)/(1) = 1`
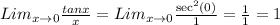
c) This also in the same indeterminate form


`Lim_ {x \rightarrow0 }\frac{ {e}^(2x) - 1 - 2x}{ {x}^(2) } = Lim_ {x \rightarrow0 } \frac{ ({e}^(2x) - 1 - 2x)'}{( {x}^(2) ) ' }`


`Lim_ {x \rightarrow0 }\frac{ {e}^(2x) - 1 - 2x}{ {x}^(2) } = Lim_ {x \rightarrow0 } \frac{ (2{e}^(2x) - 2)}{ 2x }`

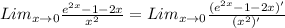
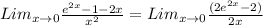
It is still of that indeterminate form so we apply the rule again, to obtain;


`Lim_ {x \rightarrow0 }\frac{ {e}^(2x) - 1 - 2x}{ {x}^(2) } = Lim_ {x \rightarrow0 } \frac{ (4{e}^(2x) )}{ 2 }`

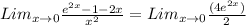
Now we have remove the discontinuity, we can evaluate the limit now, plugging in zero to obtain;


`Lim_ {x \rightarrow0 }\frac{ {e}^(2x) - 1 - 2x}{ {x}^(2) } = \frac{ (4{e}^(2(0)) )}{ 2 }`

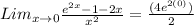
This gives us;


`Lim_ {x \rightarrow0 }\frac{ {e}^(2x) - 1 - 2x}{ {x}^(2) } =( (4(1) ))/( 2 )=2`

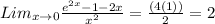
d)
`Lim_ {x \rightarrow +\infty }√(x^2+2x)-x`

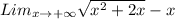
For this kind of question we need to rationalize the radical function, to obtain;


`Lim_ {x \rightarrow +\infty }(2x)/(√(x^2+2x)+x)`

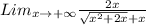
We now divide both the numerator and denominator by x, to obtain,


`Lim_ {x \rightarrow +\infty }\frac{2}{\sqrt{1+(2)/(x)}+1}`

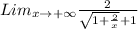
This simplifies to,


`=(2)/(√(1+0)+1)=1`