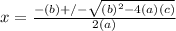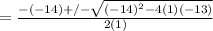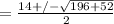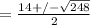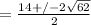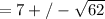Question

How do I find the zeros of x^4-10x^3-66x^2-94x-39

Answer 1

Answer: x = -1, -3, 7 + √62, 7 - √62

Explanation:

q p

x⁴ - 10x³ - 66x² - 94x - 39

`(p)/(q)` = +/-
`(1*3*13*39)/(1)`

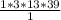
possible rational factors: 1, -1, 3, -3, 13, -13, 39, -39

Use synthetic division or long division to see which factor will leave a remainder of 0.

try x + 1 = 0 ⇒ x = -1

-1 | 1 -10 -66 -94 -39

| ↓ -1 11 55 39

1 -11 -55 -39 0

(x + 1)(x³ - 11x² - 55x - 39)

next, try x + 3 = 0 ⇒ x = -3 for the new polynomial

-3 | 1 -11 -55 -39

| ↓ -3 42 39

1 -14 -13 0

(x + 1)(x + 3)(x² - 14x - 13)

Lastly: find the zeros by setting each factor equal to zero and solve.

x + 1 = 0 ⇒ x = -1

x + 3 = 0 ⇒ x = -3

x² - 14x - 13 = 0

`x = \frac{-(b) +/- \sqrt{(b)^(2) -4(a)(c)}}{2(a)}`

`= \frac{-(-14) +/- \sqrt{(-14)^(2) -4(1)(-13)}}{2(1)}`

`= (14 +/- √(196+52))/(2)`

`= (14 +/- √(248))/(2)`

`= (14 +/- 2√(62))/(2)`

`= 7 +/- √(62)`