Question

Which expression shows the distance on a number line between -12 and-1

Answer 1

|-12-(-1)| or |-1-(-12)|

Explanation:

If a and b are two points lie on a number line, then the distance between a and b is defined by the expression |a-b| or |b-a|.

We need to find an expression that shows the distance on a number line between -12 and -1.

Here a = -12 and b = -1. So, the distance between -12 and -1 is defined by the expression

`|-12-(-1)|`

On simplification we get

`|-12+1|`

`|-11|`

`11`

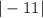
The required expression can be written as |-1-(-12)|.

Therefore the required expression is |-12-(-1)| or |-1-(-12)|, and the distance between -12 and -1 is 11 units.

Answer 2

The distance between A and B = |B - A|

We have -12 and -1.

Substitute:

|-1 - (-12)| = |-1 + 12| = |11| = 11

Answer: 11 units.