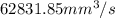Question

The radius of a sphere is increasing at a rate of 2 mm/s. How fast is the volume increasing when the diameter is 100 mm?

Answer 1

Volume increasing rate =
`62831.85 mm^3/s`

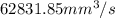
Step-by-step explanation:

We rate of change of radius of sphere,
`(dr)/(dt) =2mm/s`

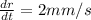
Diameter of sphere = 100 mm

Radius of sphere = 50 mm

Volume of sphere, V =
`(4)/(3) \pi r^3`

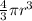
Rate of change of volume =
`(dV)/(dt)`

`(dV)/(dt)=(d)/(dt) ((4)/(3) \pi r^3)=(4)/(3) \pi(d)/(dt)(r^3)=(4)/(3) \pi*3r^2*(dr)/(dt)`

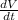
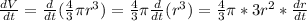
Substituting known values

`(dV)/(dt)= (4)/(3)* \pi*3*50^2*2=62831.85 mm^3/s`

Volume increasing rate =
`62831.85 mm^3/s`