Answer:
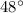
Explanation:
Consider we need to find
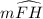 ,
,
Since, if two chords of a circle intersect outside the circle then the measure of intercepted angle is half of the difference of the measures of intercepted arcs.
Thus,

By the diagram,
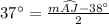
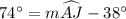
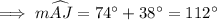
Now,
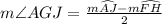
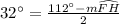

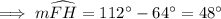
Hence, SECOND OPTION would be correct.