Question

NO LINKS!!! Please assist me part 3a

Plot the points in the coordinate plane. Then determine whether AB and CD are congruent. Explain ​

Answer 1

AB and CD are congruent.

Explanation:

Given points:

• A = (4, 1)
• B = (2, 6)
• C = (-2, 2)
• D = (-4, -3)

To determine if AB and CD are congruent, calculate the length of the two lines using the distance formula.

`\boxed{\begin{minipage}{7.8 cm}\underline{Distance Formula}\\\\$d=√((x_2-x_1)^2+(y_2-y_1)^2)$\\\\where $(x_1,y_1)$ and $(x_2,y_2)$ are the two endpoints.\end{minipage}}`

`\begin{aligned}\implies AB & = √((x_B-x_A)^2+(y_B-y_A)^2)\\& = √((2-4)^2+(6-1)^2)\\& = √((-2)^2+(5)^2)\\& = √(4+25)\\& = √(29)\end{aligned}`

`\begin{aligned}\implies CD & = √((x_D-x_C)^2+(y_D-y_C)^2)\\& = \sqrt{(-4-(-2))^2+(-3-2)^2\\& = √((-2)^2+(-5)^2)\\& = √(4+25)\\& = √(29)\end{aligned}`

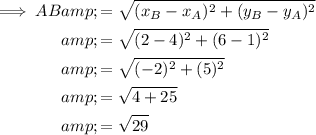
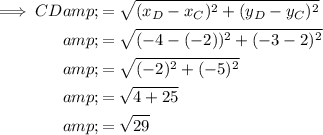
Therefore, as AB = CD, we can conclude that AB and CD are congruent.