Answer:
Fractional part of the mixed number is
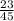 .
.
Explanation:
First we have to simplify the given expression,
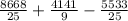
=

=
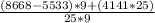
=
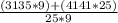
=

=
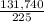
=
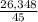
=

Now we have to take the whole number that we get by dividing numerator by denominator,
It is 585
Now we have to find the remainder after taking the numerator,
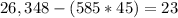
Now we represent the whole number and the fraction of remainder together as a mixed number.
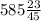
Therefore, fractional part of the mixed number is
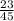 .
.