Question

A bag of marbles contains 7 red, 5 blue, 4 green, and 2 yellow marbles. Jon selects a marble, replaces it, then selects another marble. What is the probability that Jon selects a red marble and then a yellow marble?

Answer 1

for the red 7 in 20 for the yellow 2 in 20

Answer 2

Answer: about 0.0432 or 4.32%

Explanation:

Given : A bag of marbles contains 7 red, 5 blue, 4 green, and 2 yellow marbles.

Total marbles = 7+5+4+2=18

Let R : Event of getting first marble as red .

Y= Event of getting second marble as yellow.

Jon selects a marble, replaces it, then selects another marble.

⇒Both events are independent .

Probability of getting first marble as red =
`P(R)=\frac{\text{Number of red marbles}}{\text{Total marbles}}`

`\\\\=(7)/(18)`

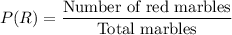
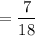
Probability of getting second marble as yellow =
`P(Y)=\frac{\text{Number of yellow marbles}}{\text{Total marbles}}`

`\\\\=(2)/(18)`

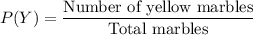
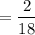
Now, the probability that Jon selects a red marble and then a yellow marble :

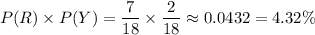`P(R)* P(Y)=(7)/(18)*(2)/(18)\approx0.0432=4.32\%` [ ∵ Event R and Y are independent .]

Hence, the probability that Jon selects a red marble and then a yellow marble is about 0.0432 or 4.32%.