Question

The table below shows the number of color pages a printer prints out over a period of time

Answer 1

Option B)
`(3)/(2)`

Explanation:

We are given the following information in the question:

A table showing the number of pages printed(y) in time(x).

x: 2 6 8 18

y: 3 9 12 27

We have to find the constant of variation.

Constant of variation

• It is the number that relates two variables that are directly proportional or inversely proportional to one another.
• y = kx, k is the constant of proportionality.

Constant of variation =

`\displaystyle(y_2-y_2)/(x_2-x_1)\\\\(x_1.y_1), (x_2,y_2)\text{ are the points belonging to the given table.}`

Putting the values, we get:

`\text{Constant of variaion} = \displaystyle(9-3)/(6-2) = (12-9)/(8-6) = (27-12)/(18-8) = (3)/(2)`

Hence, the constant of variation is
`(3)/(2)`

Answer 2

The constant of proportionality is 3/2

B is correct.

Explanation:

We are given a table of Time (x) and Number of pages (y)

In x minutes printer prints y number of pages.

As we know the it would be direct proportion because if time increase number of printing page increase.

Thus, y=kx

x is time ( independent variable)

y is number of pages (dependent variable)

k is constant of proportionality.

From table we will take the value of x and y and to solve for k

x=2, y=3

3=2k

`k=(3)/(2)`

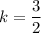
Hence, The constant of proportionality is 3/2