Question

If ANYONE could help ASAP Pls

Answer 1

ANSWER

The correct answer is C

Step-by-step explanation

This is the composition the two functions

We have


`a(x) = 3x + 1`

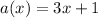
and


`b(x) = √(x - 4)`


`(b \circ \: a)(x) = b(a(x))`


`(b \circ \: a)(x) = b(3x + 1)`

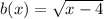
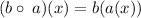
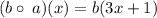
We substitute to obtain,


`(b \circ \: a)(x) = √((3x + 1) - 4)`


`(b \circ \: a)(x) = √(3x - 3)`

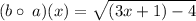
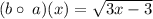
The domain of this function can be found by solving,


`3x - 3 \geqslant 0`

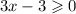
This implies that


`3x \geqslant 3`

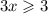
Or


`x \geqslant 1`

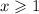
In interval notation, we have,


`[1, \infty )`

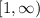
The correct answer is option C