SOLUTION TO QUESTION 1
For

We add
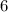 to both sides of the inequality. This gives us
to both sides of the inequality. This gives us
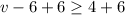
We simplify to obtain;
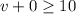
Hence,

See the attachment for graph.
SOLUTION TO QUESTION 2
For the inequality

We divide both sides by
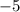 and reverse the inequality sign because, we are dividing by a negative number. This implies that;
and reverse the inequality sign because, we are dividing by a negative number. This implies that;

We simplify to get,
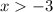
See attachment for graph
SOLUTION TO QUESTION 3
For
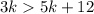
We group the terms in
 on the left hand side of the inequality,
on the left hand side of the inequality,

We simplify to obtain;
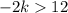
We divide both sides by
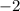 and reverse the inequality sign because, we are dividing by a negative number again. This implies that;
and reverse the inequality sign because, we are dividing by a negative number again. This implies that;
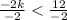
This simplifies to;

See attachment for graph.
SOLUTION TO QUESTION 4
Given the set {5,10,15}
All the possible subsets are;
{}, {5}, {10}, {15}, {5,10}, {5,15}, {10,15}, and {5,10,15}
SOLUTION TO QUESTION 5
For
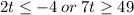
We divide through the first inequality by 2 and the second inequality by 7 to obtain;
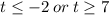
Or
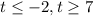
SOLUTION TO QUESTION 6
We have

This implies that;
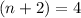 or
or
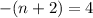
This implies that;
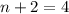 or
or
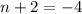
This simplifies to;
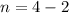 or
or
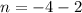
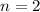 or
or

SOLUTION TO QUESTION 7
We have
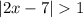
This implies that;
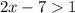 or
or

We divide the second inequality by negative 1 and reverse the inequality sign.
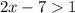 or
or
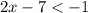
We group like terms to get,
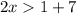 or
or
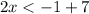
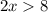 or
or
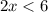
We divide both inequalities by 2 to obtain;
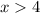 or
or
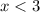
SOLUTION TO QUESTION 8
Given A={1,2,3,4,5,6,7,8,9}
and
B={2.4,6,8}
The union of A and B, are the elements in set A or set B or both.
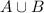 ={1,2,3,4,5,6,7,8,9}
={1,2,3,4,5,6,7,8,9}
SOLUTION TO QUESTION 9
Given:
P={1,5,7,9,13}
R={1,2,3,4,5,6,7}
and
Q={1,3,5}
We apply our understanding of subsets to draw the Venn diagram.
See attachment for the Venn Diagram.