Question

Jordan works in a science lab where he is studying the behavior of a certain unstable isotope. He has 240 milligrams of the sample, and the amount of the substance remaining in the sample decreases at a rate of 8% each day. After t days, there are less than 115 milligrams of the substance remaining. Which inequality represents this situation, and after how many days will the amount of the sample be less than 115 milligrams?

Answer 1

After 8.82 days the amount of substance is less than 115 milligrams

Explanation:

If x (t) represents the amount of substance in the sample after t days. So

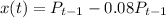`x(t) = P_(t-1)- 0.08P_(t-1)` with
`t \geq 1`

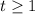
Where Pt is the amount of substance in the sample on day t.

`x (1) = 240 -0.08(240)\\ x (2) = 240 -0.08(240) - 0.8 [240 -0.08(240)]`

Then x (t) can be written as:

`x (t) = 240(1-0.08) ^ t`

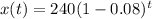
After t days there are less than 115 milligrams of the substance, then:

x (t) <115

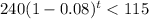`240(1-0.08) ^ t <115` This is the inequality that the situation represents.

Now we clear t.

`(0.92) ^ t <0.4792\\ t * ln (0.92) <ln (0.4792)\\\\ t>(ln (0.4792))/(ln (0.92))\\\\ t> 8,823`

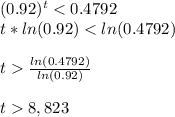
After 8.82 days the amount of substance is less than 115 milligrams