Question

Error Analysis. Find and Correct ALL 3 of the errors in the proof.( 3 points)

Answer 1

Answer: The correct reason for
`\angle4\cong \angle7` is property of corresponding angles and the reason for
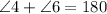`\angle4+\angle6=180` is substitute
`\angle7=\angle4` and the third error is the forget the property that the sum of consecutive interior angles is 180.

Step-by-step explanation:

It is given that m is parallel to n.

When two parallel lines intersected by a transversal eight angles are produced as shown in the given figure, where m and n are parallel and l is the transversal line.

In this case corresponding angles are congruent. Example
`\angle1\cong \angle5`,
`\angle2\cong \angle6` etc.

So,
`\angle4\cong \angle7` by the property of corresponding angles.

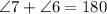`\angle7+\angle6=180` because these are supplementary angles.

Substitute
`\angle7=\angle4`

`\angle4+\angle6=180`

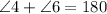
So, the correct reason is substitution.

Hence proved
`\angle4+\angle6=180`

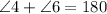
The third error is the forget the property that the sum of one side interior angles is 180. Since the alternate interior angles are congruent therefore the consecutive interior angles are supplementary angles around the sum of consecutive interior angles is 180 degree.